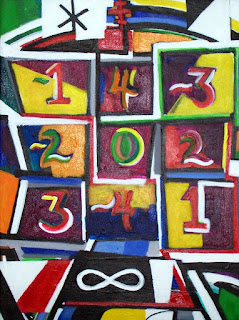Ancient Seven

Ancient Seven; a/c, 18" x 24"

Commentary on Mystic Square

The so-called "magic squares" consist of a grid of various numbers of rows and columns wherein no matter which way one adds the numbers the sum is always the same.  It becomes more complicated as the numbers and rows increase.

Mystic Square is a simple 3 x 3 gridwork wherein the sum is always "0" regardless whether one moves horizontally, vertically, or diagonally through any series of three numbers.

The Nothing as a beginning leading to the Unbounded or Infinity is a religious perspective in more than one culture.

Magic Squares or Mathematical Squares

Mystic Square; a/c, 18" x 24"

Commentary on Eddington's Glome etc.

I thought of painting Eddington's Glome after reading an essay by Arthur Eddington.  He had described, or attempted to do so, the image of a four-dimensional sphere.  I figured it would be interesting to paint a flat image using his explanation.  Also, a quote by Eddington enlightens: "We are bits of stellar matter that got cold by accident, bits of a star gone wrong."

A Level Meeting Place begins at the edges as a flat, two-dimensional work then becomes three-dimensional, though impossibly so.

The last painting, Prize of Pythagoras, is based loosely on the 3/4/5 right triangle and the Pythagorean tetrakys (think of the set-up of bowling pins) wherein ten points make up a triangle.  What I have done here is to distribute the ten points among the triangles from one to four each.

Geometry and Impossible Objects...Again!

A Level Meeting Place; a/c, 24" x 18"

Prize of Pythagoras; a/c, 24" x 18"

A Flat Version of a 4-D Sphere



Eddington's Glome; acrylic on canvas, 18" x 24"